Central Limit Theorem Formula

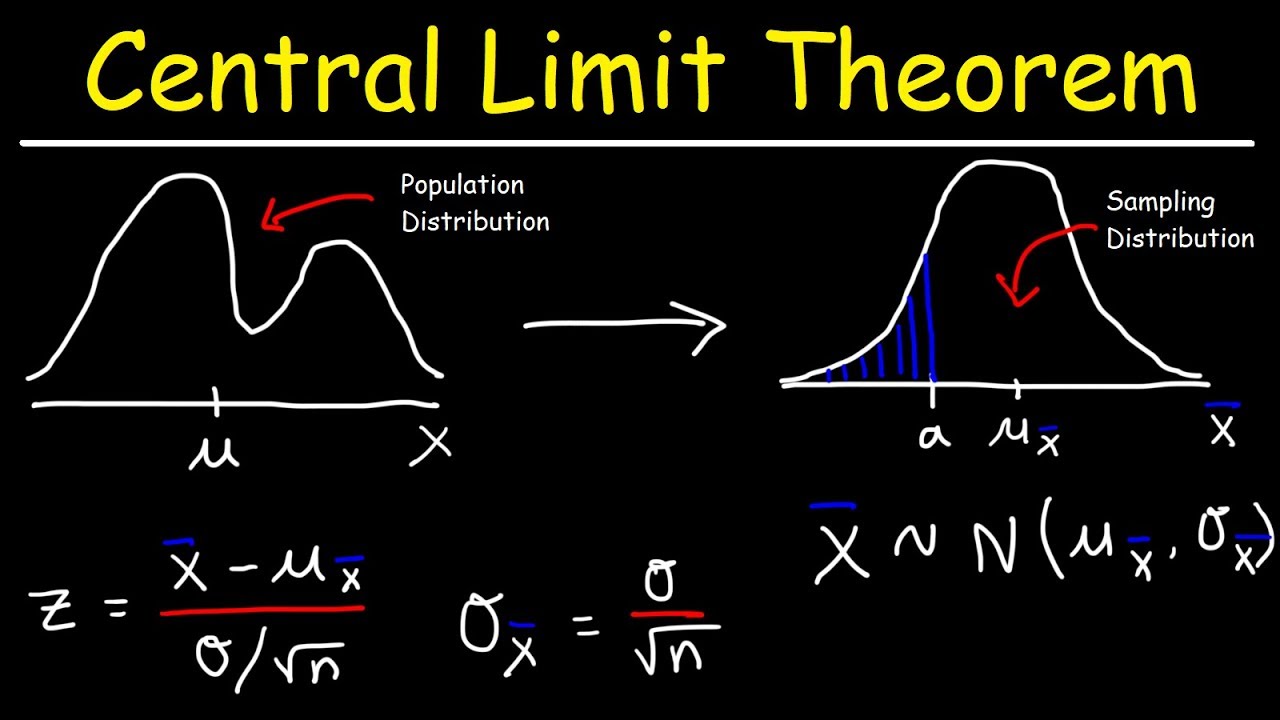
By bc.569humbertobarron 17 Sep, 2022 Post a Comment

The central limit theorem states that if the sample size is large enough even if the population distribution is abnormal the sample. Where μ Population mean.

Central Limit Theorem Formula Calculator Excel Template

The confidence level represents the long-run proportion of corresponding CIs that contain the true.

. A formal statement of the Central Limit Theorem is the following. The probability that the sample mean age is more than 30 is given by P X 30 P X 30 normalcdf 30E993415 09962. Where σ is the population standard deviation and n is the sample size.

Then f is a real valued function whose maximum over all non-negative non-zero vectors x is the PerronFrobenius eigenvalue. The binomial distribution is approximately normal with mean and variance. When omitted h is taken to be 1.

In statistics simple linear regression is a linear regression model with a single explanatory variable. O teorema central do limite ou teorema do limite central é um importante resultado da estatística e a demonstração de muitos outros teoremas estatísticos dependem deleEm teoria das probabilidades esse teorema afirma que quando o tamanho da amostra aumenta a distribuição amostral da sua média aproxima-se cada vez mais de uma distribuição normal. The standard deviation is a measure of the spread of the data from the mean value.

Then the ellipse is a non-degenerate real ellipse if and only if C 0. Regular polygons may be either convex star or skewIn the limit a sequence of regular polygons with an increasing number of sides approximates a circle if the perimeter or area is fixed or a regular apeirogon. It is not possible to define a density with reference to an.

Central Limit Theorem Formula. The formula for central limit theorem can be stated as follows. Lets read to understand the different types and examples of this phrase.

μ x Sample mean. If we assign a value of 1 to left-handedness and a value of 0 to right-handedness the probability distribution of left-handedness for the population of all humans looks. That is A backward difference uses the function values at x and x h instead of the.

This free calculator uses the central limit theorem formula to provide step-by-step calculations. S σ n. What Is the Formula for Central Limit Theorem.

ASCII characters only characters found on a standard US keyboard. As sample means are gathered from the. This means that the variable is distributed N.

Given the population standard deviation and the sample size the sample standard deviation s can be calculated using the following central limit theorem formula. To distinguish the degenerate cases from the non-degenerate case let be the determinant. The mean of the sampling distribution will be equal to the mean of the.

The Polish mathematician Kazimierz Kuratowski provided a characterization of planar graphs in terms of forbidden graphs now known as Kuratowskis theorem. Central limit theorem and the normality assumption. The central limit theorem also states that the sampling distribution will have the following properties.

If is the mean of a random sample X 1 X 2. The central limit theorem doesnt have its own formula but it relies on sample mean and standard deviation. Approximately 10 of people are left-handed.

The central limit theorem is vital in statistics for two main reasonsthe normality assumption and the precision of the estimates. A function with the form of the density function of the Cauchy distribution was studied geometrically by Fermat in 1659 and later was known as the witch of Agnesi after Agnesi included it as an example in her 1748 calculus textbook. We can use the central limit theorem formula to describe the sampling distribution.

A key characteristic of the central limit theorem is that the average of the sample mean and sample standard deviation will approximate the population mean and population standard deviation. A forward difference denoted of a function f is a function defined as Depending on the application the spacing h may be variable or constant. Both a researchers notion of how closely the sampling distribution needs to approximate.

Three basic types are commonly considered. A finite graph is planar if and only if it does not contain a subgraph that is a subdivision of the complete graph K 5 or the complete bipartite graph K 33 utility graph. For any measurable set.

Must contain at least 4 different symbols. A subdivision of a graph results from inserting. Get 247 customer support help when you place a homework help service order with us.

Applications of Central. The last formula is valid also for any non-integer. Check Central Limit Theorem proof along with solved examples.

The central limit theorem also implies that certain distributions can be approximated by the normal distribution for example. If C 0 we have an. Forward backward and central finite differences.

In analytic geometry the ellipse is defined as a quadric. σ x Sample standard deviation. In this article we will learn more about the central limit theorem its formula proof various applications and examples.

X n of size n from a distribution with a finite mean and a finite positive variance ² then the distribution of W is N01 in the limit as n approaches infinity. The central limit theorem states that the sampling distribution of a sample mean is approximately normal if the sample size is large enough even if the population distribution is not normal. The set of points of the Cartesian plane that in non-degenerate cases satisfy the implicit equation provided.

The formula of central angle is Central Angle. Despite its name the first explicit analysis of the properties of the Cauchy distribution was published by the French. Central Limit Theorem CLT states that the sampling distribution of the sample means approaches a normal distribution as the sample size is larger.

The 95 confidence level is most common but other levels such as 90 or 99 are sometimes used. In Euclidean geometry a regular polygon is a polygon that is direct equiangular all angles are equal in measure and equilateral all sides have the same length. The central limit theorem is applicable for a sufficiently large sample size n30.

The central limit theorem states that for large sample sizesn the sampling distribution will be approximately normal. In this article students can learn the central limit theorem formula definition and examples. σ Population standard deviation.

Theres no formula or calculation that spits out this number. In frequentist statistics a confidence interval CI is a range of estimates for an unknown parameterA confidence interval is computed at a designated confidence level. N Sample size.

For all non-negative non-zero vectors x let fx be the minimum value of Ax i x i taken over all those i such that x i 0. 6 to 30 characters long. If the central angle of a circle is 824 and the arc length formed is 23 cm then find out the radius of the circle.

What is the Central Limit Theorem. Given Arc length 23 cm. In the continuous univariate case above the reference measure is the Lebesgue measureThe probability mass function of a discrete random variable is the density with respect to the counting measure over the sample space usually the set of integers or some subset thereof.

That is it concerns two-dimensional sample points with one independent variable and one dependent variable conventionally the x and y coordinates in a Cartesian coordinate system and finds a linear function a non-vertical straight line that as accurately as possible predicts. We will guide you on how to place your essay help proofreading and editing your draft fixing the grammar spelling or formatting of your paper easily and cheaply.

Central Limit Theorem Clt Definition